Presentation of the project

Introduction

The motion of the human body is one of the harder things to modelise when you want to create a digital twin. When you want realistic representation of a human or any creature, it is really commun to use motion capture to capture with a high precision the movement of the member of a human. It work really well to obtain the data motion of the skeleton, but the way the skin will move with classical weighting technic implies wrong motion of the boy, especially for the shoulders and the forearm. On top that you want capt the motion of skin due to the dynamic of the muscle, their inertia and their contraction. The solution to obtain a precise motion of the human body is to use musculo-squeletal simulation which consist to modelize the skeleton, the muscle system, the skin and simulate how they interact together.

When you regard to an animals, a cow for example, when she move, even a slightly movement like eating, moving the mouth, walkin, you can see all the underneath layer of muscle and skel moving trought the skin. The kind of movement take a really long time to recreate with animation method (armature bones, and shapekeys). For more complexe and dynamic movement, the jiggle effect/ inertia of muscles and skin will appears and create a satisfying. jiggle can be use to a sensation of a massif creature, it can be a tool which convey a strong message to the spectateur.

This is already done by the industries for more than 10 years to create stunning looking VFX. Nowaday, with the democratisation of GPU computation and their improvement, real-time musculo-squeletal simulation is now envisageable. It can be used for preview of more complexe musculo-squeletal simulation or for video-game.

Finally, the main reason of this project is just because I wanted to work on human body simulation !

Related Work

Weta tissue, ZifavX, ILM'zeno and Houdini. For now, musculo-squeletal simulation are essentialy used for VFX, mainly to modelise animals. It can be used for some part of important caracter, or monster in big AAA films. The 3 software use FEM(Finite Element Method) to compute the motion of muscles. They also compute cloth simulation solver to obtain the movement of fascia and skin.

They need to compute the 3D thetraedric mesh, to be able to simulate motion of the inner point.

In VFX industry, the result of the simulation don't have to be very precise. We are juste looking for a good looking result. Contrairement à the material engineering, we can use really low meshes or use stronger hypothesis.

Method

Dynamic simulation

Muscle

To minimize the quantity of computation point, the 1 dimension FEM method is used. As most of the muscle have a slender geometry, the hypothesis of the beam theory apply. Those hypothesis include the small deformation (10°) which won't always be respected. (FAUX si j'update la geometrie a chaque pas de temps, la condition est qu'il ne faut pas une deformation de plus de 10° entre chaque pas de temps. Ce qui sera respecté).

Like any other FEM method, a elementary shape have to choosen. For 1 dimensional FEM, there not a lot of choice, the muscle will be separated a multitude of wire elementary element with 2 integrations points.

[Photo de l'élément élémentaire]

figure1: scheme representing the mesh of a muscle, and the structure of beam element at the middle, with the little cross

parler de l'intégration avec des polynomes de lagranges, de degrés 1 => que certaine grandeur ne sont pas résolut exactement et des approximation non négligeable sont effectuée (cf. shearlocking)

Et introduire, q, l'inconnu qui est dans TOUTES les prochaines équations

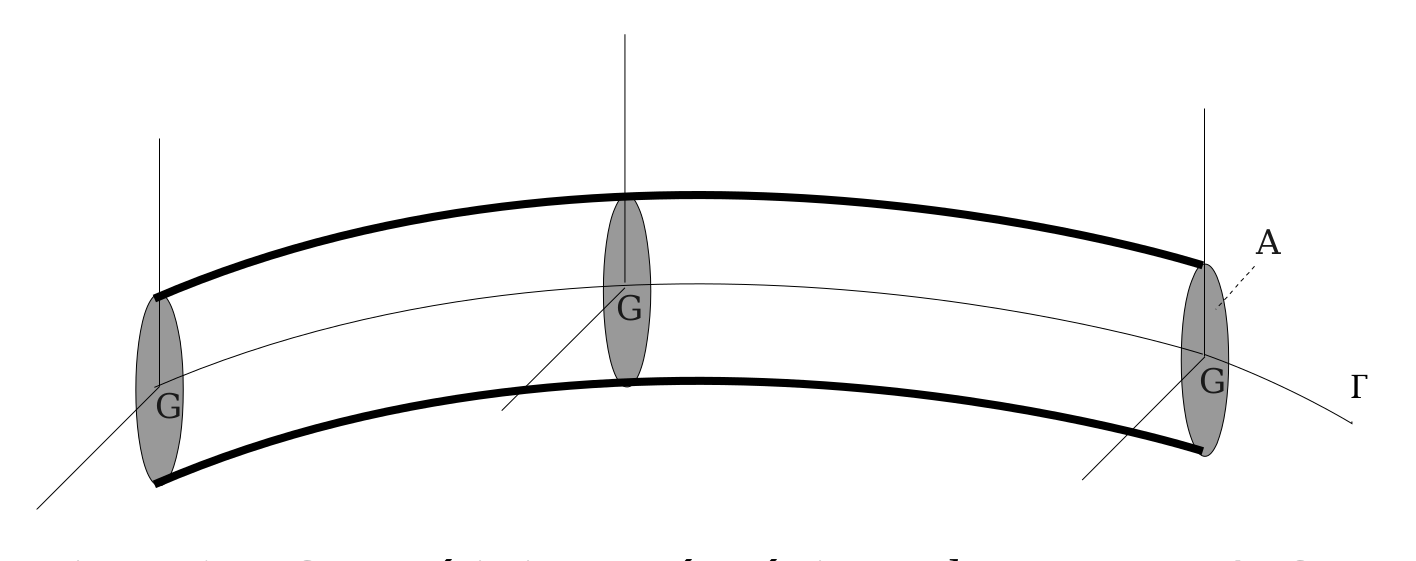
The 1D FEM method use the beam theory to reduce to 1 space variable in the mechanical equations, which them will be solved with the FEM method. In beam theory, the geometry is represented by a middle curve $\Gamma$ and a plane section $A$. The tridimensional geometry is generate by the extrusion of the $A$ section along the curve $\Gamma$.

(image a refaire)

The section $A$ won't be affected by the deformation, $i.e.$ The deformation will only depend of the position along $\Gamma$. That means that the section $A$ will have the movement of a rigid body. We can write this hypothesis as:

$$\vec{U}(x,y,z) = \vec{U}(x) + \vec{\Omega}(x) \wedge \vec{GM} \qquad \text{where} \; \Omega \; \text{is the rotation vector}$$

From this approximation, we can develop the continuous mechanical equations to obtain a relation between wire element point position and rotation and forces.

Starting with the principal of virtual work:

$$\delta \overline{W_{acc}} - \delta \overline{W_{int}} = \delta \overline{W_{ext}}$$

$$\sum_{e} \ddot{q}^{t} \int_{-1}^{1} N^t.\tilde{M_{e}}.N det(J) d\xi \:.\: \overline{q} + \sum_{e} q^{t} \int_{-1}^{1} B^t.D_{e}.B det(J) d\xi \:.\: \overline{q} = \sum_{e} \int_{-1}^{1} P_{e}.N det(J) d\xi \:.\: \overline{q}$$

The follwing matrix system can be obtain:

$$M.\ddot{q}+ K.q = P$$

The scheme in space is done, and we now look for the time scheme. A classical finite difference scheme is used. I would like to use a scheme which contain some numerical viscosity to insure stability of the simulation, and add some artificial damping to the system. That is why the scheme $f(\Delta t, q^{n+1}, q^n, q^{n-1})$ is used:

The scheme as been construct so he respected the following expression:

$$f(\Delta t, q^{n+1}, q^n, q^{n-1}) \approx \frac{d²q}{dt²} - 2 \Delta t \frac{dq}{dt}$$

This condition assure also the consistancy of the scheme and impose the scheme is $1^st$ order, $i.e.$:

$$\frac{d²q}{dt²} = f(\Delta t, q^{n+1}, q^n, q^{n-1}) + O(\Delta t)$$

The following scheme respect thoses conditions:

$$f(\Delta t, q^{n+1} q^n, q^{n-1}) = \frac{(1+\Delta t^2)q^{n+1} - 2q^n + (1+\Delta t^2)q^{n-1}}{\Delta t^2}$$

Using the scheme above, we can obtain a matrix system that have to be solve at every time step:

$$A.q^{n+1} = b(q^n, q^{n-1}) \\$$

Finally, at every time step, the following sparse matrix system is solved with the sparse GMRes solveur from the Eigen library

(link TODO): [Ca serait ouf que je puisse utiliser mon GMRes... a voir !]

Note

The above equation isn't the exact equation solved in Simuscle. Somes equations have to be added to take into account the constraints.

To simulate the motion of the muscles, 1 Dimension FEM method is used. For now it modelise several beam elements links together. On the current model, the material is isotrope, the fiber aren't taked in acount and the section is supposed circular and constant along the muscle. But the method could be improved to modelise anistrope beam element, and a custom section which will variéer. And it could be interessing to explore the isotrope beam element to modelise the fiber of the muscles.

The comportement law used is the classical hook law, but I will see if it is possible to use an exponential hook law, usually used to modelised muscules and tendon [cite]

The muscles will be considered with a constant volume to achieave it, the geometry will be inflate (flame equation) to preserve the volume. Another possibility is to scale the geometry along xy along each beam element according to the x deformation such to assure the poisson ration.

To add muscle activation force, we have to change the $\epsilon_{0}$, which apply adding a force terme to the system.

todo

For flat muscles like dorsale or abdo, the beam model would make too much assumption. A flat 2D FEM model will be elaborate.

Skin

To compute the skin dynamic, a classical spring-mass model used to made cloth simulation is implemented.[cite] 2D FEM simulation could be explore, but it is not a priority.

Bone

The Bone are rigid body which follow the motion of the armature from the BVH.

Collision detection

Muscle:

To have fast collision detection, the muscles surface is defined by a signed distance function. The muscles will collide with bones, skin and the other muscles

Muscle-Muscle: explain what happend, and the computation done for each muscles.

Muscle-Bone: same

Muscle-Skin: The point of the skin mesh will look for a collision with the sdf, and a hertz forces will be applied. (or signorini condition, but I will need to used Lagrange equation and an optimiser to compute skin movement).

Skin and bone

The skin surface is represent by a mesh and they will collide with the muscles The bones is also represent by a mesh and will collide with the muscles.

Note that for now, there is no collision between skin and bones (That implies false skin deformation on elbow, acromium, wrist) To reduce computation time, the user will be able to select the vertex(or faces) where the collision will happen between the skin and the bone.

Skin-Bone: for each point of the skin, we will check if there is a coollision for each point of the bone (Must do a BVH if I implment such a collision...).

Collision response

Testing

Future work

Simuscle is a software which relalise the computation part of the 3D Pipeline. It is centered around creature and character simulation. My goal is to gather all the require tools for making CFX (Creature/Character Visual Effect). For now, I focus on musculo-squeletal simulation but I also plan to integrated hair and cloth simulation in it. The input data, is an animation of a musculo-squeletal model of a creature, and Simuscle will compute the mesh cache which will be sent to the render.

Simuscle is developed on linux in C++, using OpenGL 4.3 for the graphic and DearImGUI for the UI. For now, Simuscle is only compatible with linux.